커리어서비스 (10.28 ~ 11.08) 진행
아래 2가지가 주요 활동이다.
1)입사지원서류 검토 상담
2)코딩테스트 준비
000 멘토님이 하루에 두 문제씩 제안을 하고 수강생이 풀어보는 방식이다.
1주일에 한번은 그 중 2문제를 골라 풀이를 Notion에 설명해 주신다.
피로도
XX게임에는 피로도 시스템(0 이상의 정수로 표현합니다)이 있으며, 일정 피로도를 사용해서 던전을 탐험할 수 있습니다. 이때, 각 던전마다 탐험을 시작하기 위해 필요한 "최소 필요 피로도"와 던전 탐험을 마쳤을 때 소모되는 "소모 피로도"가 있습니다. "최소 필요 피로도"는 해당 던전을 탐험하기 위해 가지고 있어야 하는 최소한의 피로도를 나타내며, "소모 피로도"는 던전을 탐험한 후 소모되는 피로도를 나타냅니다. 예를 들어 "최소 필요 피로도"가 80, "소모 피로도"가 20인 던전을 탐험하기 위해서는 유저의 현재 남은 피로도는 80 이상 이어야 하며, 던전을 탐험한 후에는 피로도 20이 소모됩니다.
이 게임에는 하루에 한 번씩 탐험할 수 있는 던전이 여러개 있는데, 한 유저가 오늘 이 던전들을 최대한 많이 탐험하려 합니다. 유저의 현재 피로도 k와 각 던전별 "최소 필요 피로도", "소모 피로도"가 담긴 2차원 배열 dungeons 가 매개변수로 주어질 때, 유저가 탐험할수 있는 최대 던전 수를 return 하도록 solution 함수를 완성해주세요.
- k는 1 이상 5,000 이하인 자연수입니다.
- dungeons의 세로(행) 길이(즉, 던전의 개수)는 1 이상 8 이하입니다.
- dungeons의 가로(열) 길이는 2 입니다.
- dungeons의 각 행은 각 던전의 ["최소 필요 피로도", "소모 피로도"] 입니다.
- "최소 필요 피로도"는 항상 "소모 피로도"보다 크거나 같습니다.
- "최소 필요 피로도"와 "소모 피로도"는 1 이상 1,000 이하인 자연수입니다.
- 서로 다른 던전의 ["최소 필요 피로도", "소모 피로도"]가 서로 같을 수 있습니다.
| k | dungeons | result |
| 80 | [[80,20],[50,40],[30,10]] | 3 |
현재 피로도는 80입니다.
만약, 첫 번째 → 두 번째 → 세 번째 던전 순서로 탐험한다면
- 현재 피로도는 80이며, 첫 번째 던전을 돌기위해 필요한 "최소 필요 피로도" 또한 80이므로, 첫 번째 던전을 탐험할 수 있습니다. 첫 번째 던전의 "소모 피로도"는 20이므로, 던전을 탐험한 후 남은 피로도는 60입니다.
- 남은 피로도는 60이며, 두 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 50이므로, 두 번째 던전을 탐험할 수 있습니다. 두 번째 던전의 "소모 피로도"는 40이므로, 던전을 탐험한 후 남은 피로도는 20입니다.
- 남은 피로도는 20이며, 세 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 30입니다. 따라서 세 번째 던전은 탐험할 수 없습니다.
만약, 첫 번째 → 세 번째 → 두 번째 던전 순서로 탐험한다면
- 현재 피로도는 80이며, 첫 번째 던전을 돌기위해 필요한 "최소 필요 피로도" 또한 80이므로, 첫 번째 던전을 탐험할 수 있습니다. 첫 번째 던전의 "소모 피로도"는 20이므로, 던전을 탐험한 후 남은 피로도는 60입니다.
- 남은 피로도는 60이며, 세 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 30이므로, 세 번째 던전을 탐험할 수 있습니다. 세 번째 던전의 "소모 피로도"는 10이므로, 던전을 탐험한 후 남은 피로도는 50입니다.
- 남은 피로도는 50이며, 두 번째 던전을 돌기위해 필요한 "최소 필요 피로도"는 50이므로, 두 번째 던전을 탐험할 수 있습니다. 두 번째 던전의 "소모 피로도"는 40이므로, 던전을 탐험한 후 남은 피로도는 10입니다.
따라서 이 경우 세 던전을 모두 탐험할 수 있으며, 유저가 탐험할 수 있는 최대 던전 수는 3입니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------
import itertools
def solution(k, dungeons):
answer = -1
p = itertools.permutations(dungeons, len(dungeons)) # 순열 생성
for i, d in enumerate(p):
tmpk = k
cnt = 0
for j, a in enumerate(d):
# print(a[0], tmpk)
if a[0] <= tmpk: # 최소 피로도 확인
cnt += 1
tmpk -= a[1] # 피로도 소모
# print(tmpk)
# print("cnt", cnt)
if answer < cnt:
answer = cnt
return answer
후보키
프렌즈대학교 컴퓨터공학과 조교인 제이지는 네오 학과장님의 지시로, 학생들의 인적사항을 정리하는 업무를 담당하게 되었다.
그의 학부 시절 프로그래밍 경험을 되살려, 모든 인적사항을 데이터베이스에 넣기로 하였고, 이를 위해 정리를 하던 중에 후보키(Candidate Key)에 대한 고민이 필요하게 되었다.
후보키에 대한 내용이 잘 기억나지 않던 제이지는, 정확한 내용을 파악하기 위해 데이터베이스 관련 서적을 확인하여 아래와 같은 내용을 확인하였다.
- 관계 데이터베이스에서 릴레이션(Relation)의 튜플(Tuple)을 유일하게 식별할 수 있는 속성(Attribute) 또는 속성의 집합 중, 다음 두 성질을 만족하는 것을 후보 키(Candidate Key)라고 한다.
- 유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
- 최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
제이지를 위해, 아래와 같은 학생들의 인적사항이 주어졌을 때, 후보 키의 최대 개수를 구하라.

위의 예를 설명하면, 학생의 인적사항 릴레이션에서 모든 학생은 각자 유일한 "학번"을 가지고 있다. 따라서 "학번"은 릴레이션의 후보 키가 될 수 있다.
그다음 "이름"에 대해서는 같은 이름("apeach")을 사용하는 학생이 있기 때문에, "이름"은 후보 키가 될 수 없다. 그러나, 만약 ["이름", "전공"]을 함께 사용한다면 릴레이션의 모든 튜플을 유일하게 식별 가능하므로 후보 키가 될 수 있게 된다.
물론 ["이름", "전공", "학년"]을 함께 사용해도 릴레이션의 모든 튜플을 유일하게 식별할 수 있지만, 최소성을 만족하지 못하기 때문에 후보 키가 될 수 없다.
따라서, 위의 학생 인적사항의 후보키는 "학번", ["이름", "전공"] 두 개가 된다.
릴레이션을 나타내는 문자열 배열 relation이 매개변수로 주어질 때, 이 릴레이션에서 후보 키의 개수를 return 하도록 solution 함수를 완성하라.
제한사항
- relation은 2차원 문자열 배열이다.
- relation의 컬럼(column)의 길이는 1 이상 8 이하이며, 각각의 컬럼은 릴레이션의 속성을 나타낸다.
- relation의 로우(row)의 길이는 1 이상 20 이하이며, 각각의 로우는 릴레이션의 튜플을 나타낸다.
- relation의 모든 문자열의 길이는 1 이상 8 이하이며, 알파벳 소문자와 숫자로만 이루어져 있다.
- relation의 모든 튜플은 유일하게 식별 가능하다.(즉, 중복되는 튜플은 없다.)
입출력 예
| relation | result |
| [["100","ryan","music","2"],["200","apeach","math","2"],["300","tube","computer","3"],["400","con","computer","4"],["500","muzi","music","3"],["600","apeach","music","2"]] | 2 |
입출력 예 설명
입출력 예 #1
문제에 주어진 릴레이션과 같으며, 후보 키는 2개이다.
1. 문제 파악
- 문제에서 주어지는 정보/키워드
- 후보키 ⇒ 유일성과 최소성을 만족하면서, 관계 데이터베이스에서 릴레이션의 튜플을 유일하게 식별할 수 있는 속성 또는 속성의 집합
- 유일성 ⇒ 릴레이션에 있는 모든 튜플이 유일하게 식별되도록하는 특성
- 최소성 ⇒ 후보키의 한 속성이라도 제외될 경우 유일성이 깨지는 특성
- 후보키 ⇒ 유일성과 최소성을 만족하면서, 관계 데이터베이스에서 릴레이션의 튜플을 유일하게 식별할 수 있는 속성 또는 속성의 집합
- 목표(출력)
- 후보키의 최대 개수
2. 아이디어 떠올리기
문제에서 제시된 대로 후보키를 파악하기 위해서는 유일성과 최소성을 올바르게 이해할 필요가 있다. 어떤 속성 혹은 속성의 조합이 유일성을 만족할지 모르기 때문에 모든 경우를 시도해봐야 한다. 어떤 속성 조합으로 튜플 개수를 세어봤을 때, 중복이 존재하지 않는다면, 유일성을 만족하는 것으로 해석할 수 있다.
추가로 최소성도 확인해야한다. 최소성이 위반되는 경우를 생각해보자. 예를 들어, 만약 1번 속성과 2번 속성으로 릴레이션의 모든 튜플을 구분할 수 있다고 해보자. 즉, 유일성을 만족한다. 이 때, 1번 속성만으로도, 모든 튜플을 명확하게 구분할 수 있다고하면, 1번 속성과 2번 속성의 조합은 후보키의 조건 중 최소성을 위반한 것이다. 이미 1번 속성만으로도 모든 튜플을 구분할 수 있는데, 불필요하게 2번 속성도 사용하기 때문이다. 따라서 최소성을 만족하려면, 현재 속성 조합에서 제거되어도 유일성이 만족하는 속성이 존재하는지 검사해야한다.
유일성과 최소성을 검사하기 위해서 주어진 모든 속성 조합을 시도해봐야하기 때문에 완전 탐색으로 해결해야한다. 실제로 조합을 사용해도 좋고, 비트마스크를 활용해볼 수 있다.
3. 코드설계
비트마스크
#✅ 모든 속성 조합별로 후보키 적합성을 검사한다.
#✅ 기존 후보키들과 비교해서 최소성 검사를 수행한다.
#✅ 최소성이 위반되면 다음 속성 조합의 후보키 검사를 진행한다.
#✅ 속성 조합을 기반으로 유일성을 검사한다.
#✅ 튜플 간 중복이 없으면 해당 속성 조합을 후보키로 선정한다.
#✅ 후보키 개수를 반환한다.
조합
#✅ 속성 개수 별로 모든 조합을 만들어서 후보키 적합성을 검사한다.
#✅ 모든 속성 조합별로 후보키 적합성을 검사한다.
#✅ 기존 후보키들과 비교해서 최소성 검사를 수행한다.
#✅ 최소성이 위반되면 다음 속성 조합의 후보키 검사를 진행한다.
#✅ 속성 조합을 기반으로 유일성을 검사한다.
#✅ 튜플 간 중복이 없으면 해당 속성 조합을 후보키로 선정한다.
#✅ 후보키 개수를 반환한다.
4. 구현
비트마스크(파이썬)
def solution(relation):
col_len = len(relation[0])
row_len = len(relation)
candidate_keys = []
#✅ 모든 속성 조합별로 후보키 적합성을 검사한다.
for cols in range(1, 1 << col_len):
minimality = True
row_set = set()
#✅ 기존 후보키들과 비교해서 최소성 검사를 수행한다.
for key in candidate_keys:
if key & cols == key:
minimality = False
break
#✅ 최소성이 위반되면 다음 속성 조합의 후보키 검사를 진행한다.
if not minimality:
continue
#✅ 속성 조합을 기반으로 유일성을 검사한다.
for r in range(row_len):
row_str = ""
for c in range(col_len):
if cols & (1 << c):
row_str += " " + relation[r][c]
row_set.add(row_str)
#✅ 튜플 간 중복이 없으면 해당 속성 조합을 후보키로 선정한다.
if len(row_set) == row_len:
candidate_keys.append(cols)
#✅ 후보키 개수를 반환한다.
answer = len(candidate_keys)
return answer
조합(파이썬)
def solution(relation):
col_len = len(relation[0])
row_len = len(relation)
candidate_keys = []
def gen_combinations(start, depth, max_depth, curr, result_combs):
if depth == max_depth:
result_combs.append(curr[:])
return
for i in range(start, col_len):
curr.append(i)
gen_combinations(i + 1, depth + 1, max_depth, curr, result_combs)
curr.pop()
for length in range(1, col_len + 1):
combinations = []
#✅ 속성 개수 별로 모든 조합을 만들어서 후보키 적합성을 검사한다.
gen_combinations(0, 0, length, [], combinations)
#✅ 모든 속성 조합별로 후보키 적합성을 검사한다.
for cols in combinations:
minimality = True
row_set = set()
#✅ 기존 후보키들과 비교해서 최소성 검사를 수행한다.
for key in candidate_keys:
if set(key).issubset(set(cols)):
minimality = False
break
#✅ 최소성이 위반되면 다음 속성 조합의 후보키 검사를 진행한다.
if not minimality:
continue
#✅ 속성 조합을 기반으로 유일성을 검사한다.
for r in relation:
row_str = ""
for c in cols:
row_str += " " + r[c]
row_set.add(row_str)
#✅ 튜플 간 중복이 없으면 해당 속성 조합을 후보키로 선정한다.
if len(row_set) == row_len:
candidate_keys.append(cols)
#✅ 후보키 개수를 반환한다.
return len(candidate_keys)
785. Is Graph Bipartite?
문제 유형 : DFS / BFS
문제 난이도 : Medium
문제
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
- There are no self-edges (graph[u] does not contain u).
- There are no parallel edges (graph[u] does not contain duplicate values).
- If v is in graph[u], then u is in graph[v] (the graph is undirected).
- The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.
A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true if and only if it is bipartite.
n개의 노드를 가진 무방향 그래프가 주어진다.
그래프의 노드들이 두 독립된집합 A와 B로 나누어지고, 서로 다른 집합끼리만 이어지는 그래프인 경우를 이분 그래프라고 할 때,
이분 그래프이면 true를, 아니면 false를 반환하라.
Example 1

Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.
DFS / BFS로 문제를 풀면 된다. 탐색을 하는 과정에 현재 노드의 색깔이 인접 노드의 색깔과 같은 경우 조건을 불만족하므로 false를 반환시키면 된다.
탐색을 마치면 true를 반환해주면 된다. 시간 복잡도는 O(V+E).
class Solution {
public:
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
vector<int> color(n, 0);
for(int node = 0; node < n; node++){
if(color[node] != 0) continue;
queue<int> q;
q.push(node);
color[node] = 1;
while(!q.empty()){
int cur = q.front();
q.pop();
for(int ne : graph[cur]){
if(color[ne] == 0){
color[ne] = -color[cur];
q.push(ne);
}else if(color[ne] != -color[cur]){
return false;
}
}
}
}
return true;
}
};322. Coin Change
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
Example 1:
Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1
Example 2:
Input: coins = [2], amount = 3
Output: -1
Example 3:
Input: coins = [1], amount = 0
Output: 0
Constraints:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
def coinChange(coins, amount):
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for coin in coins:
for i in range(coin, amount + 1):
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
# Test cases
coins1 = [1, 2, 5]
amount1 = 11
print(coinChange(coins1, amount1))
# Output: 3
coins2 = [2]
amount2 = 3
print(coinChange(coins2, amount2))
# Output: -1
coins3 = [1]
amount3 = 0
print(coinChange(coins3, amount3))
# Output: 0
연구소
문제
인체에 치명적인 바이러스를 연구하던 연구소에서 바이러스가 유출되었다. 다행히 바이러스는 아직 퍼지지 않았고, 바이러스의 확산을 막기 위해서 연구소에 벽을 세우려고 한다.
연구소는 크기가 N×M인 직사각형으로 나타낼 수 있으며, 직사각형은 1×1 크기의 정사각형으로 나누어져 있다. 연구소는 빈 칸, 벽으로 이루어져 있으며, 벽은 칸 하나를 가득 차지한다.
일부 칸은 바이러스가 존재하며, 이 바이러스는 상하좌우로 인접한 빈 칸으로 모두 퍼져나갈 수 있다. 새로 세울 수 있는 벽의 개수는 3개이며, 꼭 3개를 세워야 한다.
예를 들어, 아래와 같이 연구소가 생긴 경우를 살펴보자.
2 0 0 0 1 1 0
0 0 1 0 1 2 0
0 1 1 0 1 0 0
0 1 0 0 0 0 0
0 0 0 0 0 1 1
0 1 0 0 0 0 0
0 1 0 0 0 0 0
이때, 0은 빈 칸, 1은 벽, 2는 바이러스가 있는 곳이다. 아무런 벽을 세우지 않는다면, 바이러스는 모든 빈 칸으로 퍼져나갈 수 있다.
2행 1열, 1행 2열, 4행 6열에 벽을 세운다면 지도의 모양은 아래와 같아지게 된다.
2 1 0 0 1 1 0
1 0 1 0 1 2 0
0 1 1 0 1 0 0
0 1 0 0 0 1 0
0 0 0 0 0 1 1
0 1 0 0 0 0 0
0 1 0 0 0 0 0
바이러스가 퍼진 뒤의 모습은 아래와 같아진다.
2 1 0 0 1 1 2
1 0 1 0 1 2 2
0 1 1 0 1 2 2
0 1 0 0 0 1 2
0 0 0 0 0 1 1
0 1 0 0 0 0 0
0 1 0 0 0 0 0
벽을 3개 세운 뒤, 바이러스가 퍼질 수 없는 곳을 안전 영역이라고 한다. 위의 지도에서 안전 영역의 크기는 27이다.
연구소의 지도가 주어졌을 때 얻을 수 있는 안전 영역 크기의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. (3 ≤ N, M ≤ 8)
둘째 줄부터 N개의 줄에 지도의 모양이 주어진다. 0은 빈 칸, 1은 벽, 2는 바이러스가 있는 위치이다. 2의 개수는 2보다 크거나 같고, 10보다 작거나 같은 자연수이다.
빈 칸의 개수는 3개 이상이다.
출력
첫째 줄에 얻을 수 있는 안전 영역의 최대 크기를 출력한다.
예제 입력 1
7 7
2 0 0 0 1 1 0
0 0 1 0 1 2 0
0 1 1 0 1 0 0
0 1 0 0 0 0 0
0 0 0 0 0 1 1
0 1 0 0 0 0 0
0 1 0 0 0 0 0
예제 출력 1
27
예제 입력 2
4 6
0 0 0 0 0 0
1 0 0 0 0 2
1 1 1 0 0 2
0 0 0 0 0 2
예제 출력 2
9
예제 입력 3
8 8
2 0 0 0 0 0 0 2
2 0 0 0 0 0 0 2
2 0 0 0 0 0 0 2
2 0 0 0 0 0 0 2
2 0 0 0 0 0 0 2
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
예제 출력 3
3
풀이
import itertools
dx,dy=[1,-1,0,0],[0,0,1,-1]
def bfs():
global mx
S=V[:]
VIS=[[0]*M for i in range(N)]
for x,y in V:VIS[x][y]=1
cnt=0
while S:
x,y=S.pop()
for i in range(4):
nx,ny=x+dx[i],y+dy[i]
if 0<=nx<N and 0<=ny<M and VIS[nx][ny]==0 and A[nx][ny]==0:
cnt+=1
VIS[nx][ny]=1
S.append((nx,ny))
return len(BLANK)-3-cnt
N,M=map(int,input().split())
A,BLANK,V=[],[],[]
for i in range(N):
A.append(list(map(int,input().split())))
for j in range(M):
if A[i][j]==0:BLANK.append((i,j))
if A[i][j]==2:V.append((i,j))
mx=0
for nCr in itertools.combinations(BLANK,3):
for i,j in nCr:A[i][j]=1
mx=max(mx,bfs())
for i,j in nCr:A[i][j]=0
print(mx)1. 문제 파악
- 문제에서 주어지는 정보/키워드
- 바이러스 ⇒ 벽으로 막히지 않은 빈 칸에 상하좌우로 전파된다.
- 벽 ⇒ 바이러스가 전파되지 못하며 새로운 벽 3개를 세울 수 있다.
- 안전영역 ⇒ 바이러스가 전부 전파된 후에 바이러스가 전파되지 못한 영역
- 목표(출력)
- 벽 3개를 세운 뒤 바이러스를 전파했을 때 가능한 최대 안전영역 넓이
2. 아이디어 떠올리기
문제에서 연구소는 암시적 그래프의 형태로 주어져 있다. 이 때 바이러스는 벽이 아닌 빈 칸에 대해서는 자유롭게 전파가 될 수 있기에 bfs 또는 dfs를 통해 바이러스의 전파 결과를 알 수 있다.
문제에서 요구하는 값은 벽 3개를 세울 때 가능한 안전영역의 최대 넓이이다. 그렇기에 빈 칸들에 대해 조합을 수행해 벽 3개를 세울 수 있는 모든 경우의 수를 구하고 bfs/dfs를 수행한 결과에서 0의 개수를 확인하면 문제를 풀 수 있다.
3. 코드설계
#✅ 입력 형식에 맞춰 입력값을 받는다.
#✅ 빈 칸과 바이러스 위치를 저장한다.
#✅ 임의의 3개의 빈 칸을 선택한다.
#✅ 선택한 3개의 빈 칸에 벽을 세운다.
#✅ 바이러스 위치를 시작으로 BFS/DFS 알고리즘을 수행한다.
#✅ 안전영역의 최대 넓이를 갱신한다.
#✅ 세웠던 3개의 벽을 다시 빈 칸으로 되돌린다.
4. 구현
파이썬
from itertools import combinations
from collections import deque, Counter
import sys
input = sys.stdin.readline
#✅ 입력 형식에 맞춰 입력값을 받는다.
n, m = map(int,input().split())
board = [list(map(int,input().split())) for _ in range(n)]
virus, empty = [], []
answer = 0
#✅ 빈 칸과 바이러스 위치를 저장한다.
for r in range(n):
for c in range(m):
if board[r][c] == 0:
empty.append([r,c])
elif board[r][c] == 2:
virus.append([r,c])
print("virus: ", virus)
print("empty: ", empty)
def in_range(next_r, next_c):
return 0 <= next_r < n and 0 <= next_c < m
def bfs():
global answer
tmp = [board[i][:] for i in range(n)]
queue = deque(virus)
while queue:
r,c = queue.popleft()
for dr, dc in [[-1,0],[1,0],[0,-1],[0,1]]:
next_r, next_c = r+dr, c+dc
if in_range(next_r, next_c):
if tmp[next_r][next_c] == 0:
tmp[next_r][next_c] = 2
queue.append((next_r,next_c))
count = Counter([])
for row in tmp:
count += Counter(row)
#✅ 안전영역의 최대 넓이를 갱신한다.
answer = max(answer, count[0])
return
#✅ 임의의 3개의 빈 칸을 선택한다.
for new_wall in combinations(empty, 3):
row, col = [], []
for r, c in new_wall:
row.append(r)
col.append(c)
if board[r][c] != 0:
break
else:
#✅ 선택한 3개의 빈 칸에 벽을 세운다.
for i in range(3):
board[row[i]][col[i]] = 1
#✅ 바이러스 위치를 시작으로 BFS/DFS 알고리즘을 수행한다.
bfs()
#✅ 세웠던 3개의 벽을 다시 빈 칸으로 되돌린다.
for i in range(3):
board[row[i]][col[i]] = 0
print(answer)
Sudoku Solver
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
1.Each of the digits 1-9 must occur exactly once in each row.
2.Each of the digits 1-9 must occur exactly once in each column.
3.Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.
The '.' character indicates empty cells.
Example 1:

Input: board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
Explanation: The input board is shown above and the only valid solution is shown below:

Constraints:
- board.length == 9
- board[i].length == 9
- board[i][j] is a digit or '.'.
- It is guaranteed that the input board has only one solution.
1. 문제 파악
- 문제에서 주어지는 정보/키워드
- board ⇒ 빈 칸에 규칙에 따라 1 ~ 9 사이의 정수를 넣기
- row ⇒ 한 행에 1 ~ 9 사이의 정수가 하나씩 채워져야함
- column ⇒ 한 열에 1 ~ 9 사이의 정수가 하나씩 채워져야함
- 3x3 sub-boxes ⇒ 3x3 크기의 정사각형에 1 ~ 9 사이의 정수가 하나씩 채워져야함
- '.' ⇒ 빈 칸
- board ⇒ 빈 칸에 규칙에 따라 1 ~ 9 사이의 정수를 넣기
- 목표(출력)
- 9x9 크기의 board 의 빈 칸을 규칙에 따라 1 ~ 9 사이의 정수로 채우기
- only one solution ⇒ 주어진 board 는 오직 1개의 정답만을 가짐
- 9x9 크기의 board 의 빈 칸을 규칙에 따라 1 ~ 9 사이의 정수로 채우기
2. 아이디어 떠올리기
문제에서 여러 제약 사항을 부여했다. board 의 크기는 9x9 로 고정이고, 반드시 1가지 정답만을 가진다. 그러면 board 의 모든 칸을 돌아볼 때, 1 ~ 9 중에서 스도쿠 규칙에 따라 1 ~ 9 중에서 어떤 숫자가 해당 칸에 적합한지 검사한다. 만약 규칙에 어긋나는 숫자를 찾는다면 다시 빈 칸으로 되돌리고 이전 칸을 다른 숫자로 채워보는 것을 반복한다. board 는 81칸으로 고정이기 때문에 충분히 백트래킹을 사용해도 문제를 해결할 수 있을 것으로 보인다.
3. 코드설계
#✅ 모든 칸에 올바르게 숫자를 부여했다면 True/true를 반환한다.
#✅ 현재 위치(i, j)가 비어있는지 검사한다.
#✅ 현재 위치에 1 ~ 9 사이의 정수를 부여해본다.
#✅ 현재 위치에 선택한 정수의 유효성을 검사한다.
#✅ board[i][j]에 유효한 정수를 부여한다.
#✅ 백트래킹을 수행한다. (재귀 함수 호출)
#✅ False가 반환되면, board[i][j]를 빈 칸으로 되돌린다.
#✅ 현재 위치(i, j)가 비어있지 않다면, 다음 위치로 넘어간다. (재귀 함수 호출)
4. 구현
파이썬
class Solution:
def solveSudoku(self, board):
"""
Do not return anything, modify board in-place instead.
"""
def check_empty(board, r, c):
if board[r][c] != ".":
return False
return True
def check_valid(board, num, r, c):
for i in range(9):
# 행 확인
if board[r][i] == num:
return False
# 열 확인
if board[i][c] == num:
return False
# 3x3 sub-box 확인
if board[(r // 3) * 3 + i // 3][(c // 3) * 3 + i % 3] == num:
return False
return True
def backtracking(board, index):
#✅ 모든 칸에 올바르게 숫자를 부여했다면 True/true를 반환한다.
if index == 81:
return True
i, j = index // 9, index % 9
#✅ 현재 위치(i, j)가 비어있는지 검사한다.
if check_empty(board, i, j):
#✅ 현재 위치에 1 ~ 9 사이의 정수를 부여해본다.
for num in map(str, range(1, 10)):
#✅ 현재 위치에 선택한 정수의 유효성을 검사한다.
if check_valid(board, num, i, j):
#✅ board[i][j]에 유효한 정수를 부여한다.
board[i][j] = num
#✅ 백트래킹을 수행한다. (재귀 함수 호출)
if backtracking(board, index + 1):
return True
#✅ False가 반환되면, board[i][j]를 빈 칸으로 되돌린다.
board[i][j] = "."
return False
#✅ 현재 위치(i, j)가 비어있지 않다면, 다음 위치로 넘어간다. (재귀 함수 호출)
else:
return backtracking(board, index + 1)
backtracking(board, 0)
합승 택시 요금
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.
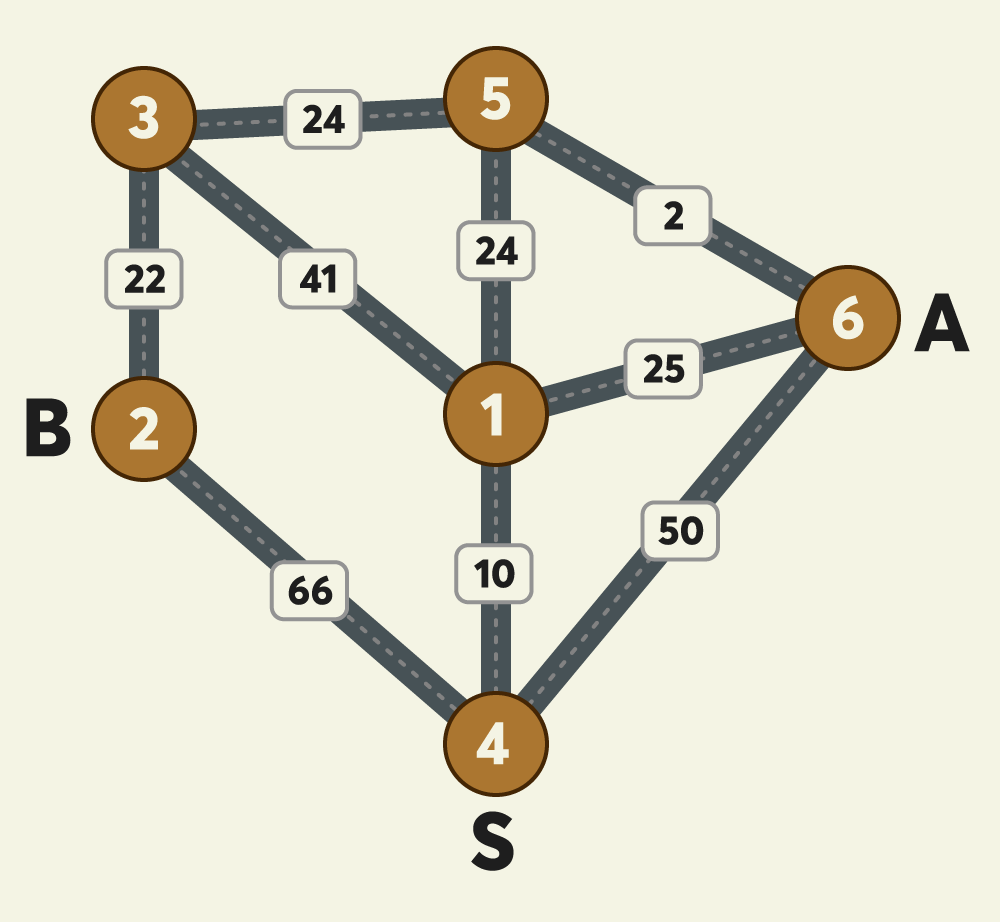
위 예시 그림은 택시가 이동 가능한 반경에 있는 6개 지점 사이의 이동 가능한 택시노선과 예상요금을 보여주고 있습니다.
그림에서 A와 B 두 사람은 출발지점인 4번 지점에서 출발해서 택시를 타고 귀가하려고 합니다. A의 집은 6번 지점에 있으며 B의 집은 2번 지점에 있고 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 합니다.
- 그림의 원은 지점을 나타내며 원 안의 숫자는 지점 번호를 나타냅니다.
- 지점이 n개일 때, 지점 번호는 1부터 n까지 사용됩니다.
- 지점 간에 택시가 이동할 수 있는 경로를 간선이라 하며, 간선에 표시된 숫자는 두 지점 사이의 예상 택시요금을 나타냅니다.
- 간선은 편의 상 직선으로 표시되어 있습니다.
- 위 그림 예시에서, 4번 지점에서 1번 지점으로(4→1) 가거나, 1번 지점에서 4번 지점으로(1→4) 갈 때 예상 택시요금은 10원으로 동일하며 이동 방향에 따라 달라지지 않습니다.
- 예상되는 최저 택시요금은 다음과 같이 계산됩니다.
- 4→1→5 : A, B가 합승하여 택시를 이용합니다. 예상 택시요금은 10 + 24 = 34원 입니다.
- 5→6 : A가 혼자 택시를 이용합니다. 예상 택시요금은 2원 입니다.
- 5→3→2 : B가 혼자 택시를 이용합니다. 예상 택시요금은 24 + 22 = 46원 입니다.
- A, B 모두 귀가 완료까지 예상되는 최저 택시요금은 34 + 2 + 46 = 82원 입니다.
[문제]
지점의 개수 n, 출발지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.
[제한사항]
- 지점갯수 n은 3 이상 200 이하인 자연수입니다.
- 지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 즉, 출발지점, A의 도착지점, B의 도착지점은 서로 겹치지 않습니다.
- fares는 2차원 정수 배열입니다.
- fares 배열의 크기는 2 이상 n x (n-1) / 2 이하입니다.
- 예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (6 x 5 / 2 = 15)
- fares 배열의 각 행은 [c, d, f] 형태입니다.
- c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
- 지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 요금 f는 1 이상 100,000 이하인 자연수입니다.
- fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, [c, d, f]가 있다면 [d, c, f]는 주어지지 않습니다.
- 출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.
1. 문제 파악
- 문제에서 주어지는 정보/키워드
- n ⇒ 지점의 개수, 노드의 개수
- s, a, b ⇒ 출발지점(합승지점), A의 도착지점, B의 도착지점
- fares[i] = [지점1, 지점2, 택시요금] ⇒ 무방향 가중치 그래프
- 목표(출력)
- 두 사람의 귀가 경로의 가장 적은 택시 비용을 구해야 한다.
- 귀가 경로는 지점 x 까지 합승할 때 s→x→a, s→x→b
- 택시 비용은 (s→x) + (x→a) + (x→b)
2. 아이디어 떠올리기
문제에서 제시하는 목표는 s 지점에서 두 승객이 택시를 탑승하여 각자의 목적지까지 갈 수 있는 최저 택시 요금을 구하는 것이다. 이 때 두 승객은 특정 지점까지 택시를 합승하여 비용을 절약할 수 있다.
이 때 x 지점까지 택시를 합승한다 하면 두 사람의 귀가 경로는 s→x→a, s→x→b가 되며 택시 비용은 cost(s→x) + cost(x→a) + cost(x→b)가 된다.
또한 해당 그래프는 무방향 그래프이기에 cost(x→a) == cost(a→x), cost(x→b) == cost(b→x)가 된다.
즉 s, a, b 3개의 지점에서 x 지점까지 도달하는 최소 비용의 합을 x 지점을 조정해가며 구하면 된다.
여기서 3개의 지점에서 x 지점까지 도달하는 최소 비용들은 다음과 같이 구할 수 있다.
우선 첫번째 방법은 3개의 지점에서 각각 다익스트라를 수행하는 것이다. 다익스트라는 시작 노드에서 각 노드까지 도달하는 최소 비용들을 반환하며 그렇기에 각 3개의 노드에서 다익스트라를 수행하면 임의의 노드 x 까지 도달하는 최소 비용을 알 수 있다.
즉 문제 상황으로 돌아오면, 3개의 지점에서 각 지점까지 도달하는 최소 비용을 저장하고 모든 지점을 순회하며 cost(s→x) + cost(x→a) + cost(x→b)의 최소값을 찾으면 문제에서 요구하는 최저 택시 요금이 나오게 된다.
3. 코드설계
#✅ 인풋을 본인이 쓰기 편한 구조로 바꾸기(다익스트라) => 무방향 그래프 만들기
#✅ s, a, b 3개의 노드에서 모든 노드까지 도달하는 최소 비용을 저장한다.
#✅ case1: s, a, b 3개의 노드에서 각각 다익스트라 알고리즘을 수행한다.
#✅ case2: 플로이드 워셜 알고리즘을 수행한다.
#✅ 모든 노드를 순회하며 cost(s->x) + cost(x->a) + cost(x->b)의 최소비용을 반환한다.
파이썬
import heapq
def solution(n, s, a, b, fares):
#✅ 인풋을 본인이 쓰기 편한 구조로 바꾸기(다익스트라) => 무방향 그래프 만들기
graph = [[] for _ in range(n+1)]
for u, v, w in fares:
graph[u].append((v,w))
graph[v].append((u,w))
answer = 100000000
#✅ s, a, b 3개의 노드에서 모든 노드까지 도달하는 최소 비용을 저장한다.
costs = [[100000000 for _ in range(n+1)] for _ in range(3)]
#✅ s, a, b 3개의 노드에서 각각 다익스트라 알고리즘을 수행한다.
for i, start_node in enumerate([s, a, b]):
heap = []
heapq.heappush(heap, (0, start_node))
costs[i][start_node] = 0
while heap:
cur_cost, cur_v = heapq.heappop(heap)
for next_v, cost in graph[cur_v]:
next_cost = cur_cost+cost
if costs[i][next_v] > next_cost:
costs[i][next_v] = next_cost
heapq.heappush(heap, (next_cost, next_v))
#✅ 모든 노드를 순회하며 cost(s->x) + cost(x->a) + cost(x->b)의 최소비용을 반환한다.
for i in range(1, n+1):
answer = min(answer, costs[0][i]+costs[1][i]+costs[2][i])
return answerimport heapq
def solution(n, s, a, b, fares):
answer = 100000000
#✅ s, a, b 3개의 노드에서 모든 노드까지 도달하는 최소 비용을 저장한다.
costs = [[0 if i==j else 1000000000 for i in range(n+1)] for j in range(n+1)]
# 플로이드 워셜 알고리즘 전처리
for u, v, w in fares:
costs[u][v] = w
costs[v][u] = w
#✅ 플로이드 워셜 알고리즘을 수행한다.
for i in range(n+1):
for j in range(n+1):
for k in range(n+1):
if costs[j][k] > costs[j][i] + costs[i][k]:
costs[j][k] = costs[j][i] + costs[i][k]
#✅ 모든 노드를 순회하며 cost(s->x) + cost(x->a) + cost(x->b)의 최소비용을 반환한다.
for i in range(n+1):
answer = min(answer, costs[s][i]+costs[i][a]+costs[i][b])
return answer
'Upstage AI Lab' 카테고리의 다른 글
| Upstage AI Lab 3기 - IR 프로젝트 테스트 내용 정리 (0) | 2024.10.24 |
|---|---|
| Upstage AI Lab 3기 - Data Centric AI (5) | 2024.10.01 |
| Upstage AI Lab 3기 - Natural Language Processing Basic, Advanced, 경진대회, LM to LLM (2) | 2024.09.22 |
| Upstage AI Lab 3기 - Computer Vision & Generation (1) | 2024.08.20 |
| Upstage AI Lab 3기 - Computer Vision [경진대회] Image Classification (0) | 2024.08.13 |


