프로젝트 수행을 위한 이론3 : Statistics
30년만에 수학, 그것도 고등학교때 관심없이 거의 건너뛰었던 통계학 이론 수업이 시작되었다.
저너머 블랙홀 속에 있는 기억을 더듬어 가며 수업을 따라 가는 나... 말은 들리는데 머리가 거부한다.
강사 : 오영석 교수
수업 목차는 아래와 같다.
[1일차]
1. Orientation
2. Number of Cases
3. Probability Theory
4. Variables & Scales
5. Population & Sample
6. Descriptive Statistics
7. Random Variable
8. Probability Distribution
9. Estimation & Test
[2일차]
1. Exercise
2. t-test
3. Analysis of Variance
[3일차]
1. Exercise
2. Correlation Analysis
3. Linear Regression
4. Binary Classification
5. Maximum Likelihood Estimation - 마지막에 추가된 내용

▣ Orientation
강사 소개
이름 : 오영석
경력 : (현) 고려사이버대학교미래학부인공지능전공외래교수
(전) 경기과학기술대학교인공지능학과강사
다수의 논문과 연구활동.....
인공지능수학, 공업수학
=> 인공지능에서 수학이 어떻게 다뤄지는지 연구
강좌 소개
- Statistics의 기초 개념과 원리, 방법을 학습
- Python을 활용하여 데이터를 표현하고 처리하는 실습
Statistics의 필요성 : 통계의 오류 예
- [아동학대] 친부모 '80%' 계부모 '10%미만' : 전체 부모 대상이므로 통계 오류
- '속도의 유혹' 곧은 길서 사고 더 많아요.
강좌의 목표
- Statistics의 기초 개념과 원리, 방법을 토대로
- 어떻게 수집한 데이터의 특성을 요약 정리할 수 있는지(기술 통계),
- 어떻게 분석한 데이터를 근거로 모집단의 특성을 추론할 수 있는지(추리 통계),
- 어떻게 불확실한 미래의 사건을 예측할 수 있는지를 학습하는 것(회귀와 분류)
Text Book 소개
- 제대로 시작하는 기초통계학
- 모두의 인공지능 기초 수학 (14~16장)
- 현대 기초통계학(이해와적용)
- 머신러닝 수학 바이블( 영문판은 무료 ) --- 고급원할 때
▣ Number of Cases
01 Rule of Sum & Rule of Product(합의 법칙 & 곱의 법칙)
1.1 Learning Objectives
1.2 Parallax Thinking(AlphaGo)
1.3 Rule of Sum
1.4 Rule of Product
02 Permutation & Combination(순열 & 조합)
2.1 Learning Objectives
2.2 Parallax Thinking 2
2.3 Permutation
2.4 Parallax Thinking 3
2.5 Combination
2.5 Learning Summary
합의 법칙
두 사건 A와 B가 상호 배타적일 때, 즉 동시에 발생할 수 없을 때, 사건 A가 일어나는 경우의 수가 m이고,
사건 B가 일어나는 경우의 수가 n이면, 사건 A 또는 사건 B가 일어나는 경우의 수의 총합은 m + n
* 서로 다른 A와 B 주사위를 동시에 던질 때, A 또는 B 주사위가 나오는 눈의 수가 3의 배수인 경우의 수
=> 4번(3,6 + 3,6)
곱의 법칙
두 독립 사건 A와 B가 있을 때, 사건 A가 일어나는 경우의 수가 m이고, 사건 A의 각각의 결과에 대하여
독립적으로 사건 B가 일어나는 경우의 수가 n이면, 두 사건 A와 B가 동시에 일어나는 경우의 수는 m×n
* 서로 다른꽃병2개와장미4송이가있을때, 꽃병에장미를꽂기위해서꽃병한개와장미한송이를동시에택하는경우의수
=> 8번
순열
서로 다른 𝑛개에서 서로 다른 𝑟개를 선택하여 일렬로 나열하는 것을 𝑛개에서 𝑟개를 택한 순열이라고 함
𝑛P𝑟=𝑛×(𝑛−1)×(𝑛−2)×⋯⋯×(𝑛−𝑟+1)
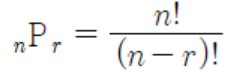
1, 2, 3, 4와같은4장의숫자카드가있을때, 2장을선택하여두자리자연수를만드는방법의수
=> 4*3*2/2 = 12
조합
서로 다른 𝑛개에서(순서를생각하지않고) 𝑟개를 선택하는 것을 𝑛개에서 𝑟개를 택한 조합이라고 함.
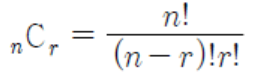
▣ Probability Theory
전체 == 표본공간
일부 == 사건
합사건: 사건A와 B에 대해 A가 발생하거나 B가 발생하는 사건
곱사건: 사건A와 B에 대해 A와 B가 동시에 발생하는 사건
배반사건: 사건A와 B에 대해A나 B 중 어느 하나의 사건이 발생하면, 다른 사건이 발생하지 않는 사건
여사건: 사건A에 대해 A가 발생하지 않는 사건
1부터10까지숫자가적힌공10개가들어있는주머니안에서공1개를뽑을때,
2의배수가나오는사건을A, 5의배수가나오는사건을B라고하면,
사건A 또는사건B가발생할확률은?
5/10 + 2/10 - 1/10= 6/10 = 3/5
확률 덧셈 법칙
두 사건 A, B가 배반사건이 아니라면 P(A∪B)=P(A)+P(B)-P(A∩B)
두 사건 A, B가 배반사건이면 P(A∪B)=P(A)+P(B)
Conditional Probability(조건부 확률)
: 사건 A가 발생한 상황하에 사건 B가 발생할 확률을 구하고자 할때,
조건부확률 : P(B l A) B given A
어느 회사의 주가가 월요일장에 상승할 확률이 0.7이라고 하며, 월요일에 상승하고
그 다음날에도 상승할 확률이 0.3이라고 한다. 어느 특정 월요일에 주가가 올랐다면
그 다음날에도 다시 주가가 오를 확률은?
=>
P(A) = 0.7
P(B) : 화요일에 상승할 확률
P(A교집합B) = 0.3
P(B|A) = 0.3/0.7 = 3/7
독립사건
=> 동전 앞이 나왔을 때 동전 뒷면이 나올 확률( P(B|A )은 둘 사건은 독립이므로 뒷면이 나올 확률( P(B) )과 같다.
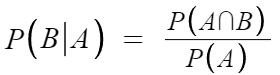
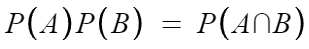
▣ Variables & Scales
Mathematical Probability => Mathematical Scales
분석을 하기 위해서 데이터는 정량적으로 수집해야 한다.
매개변수란 연구에서 통제되어야 할 변수를 의미함
예) A교수법과 B교수법(독립변수)에 따른 어휘력(종속변수)차이 연구에서 아동의 지능(매개변수)
척도
범주형 척도 vs 연속형 척도
- 명목척도, 서열척도
- 등간척도, 비율 척도
리커트척도 : 등간 척도라 보기에 애매함 (좋음 아주좋음 보통)
등간 척도 : 온도
비율 척도 : "없다" 개념이 존재해야 함
길이 무게 부피
▣ Population & Sample
분산 : 데이터가 얼마나 퍼져 있는지
표준편차 : 루트(분산)
편의표본추출: 연구자 편의에 따라 추출
모집단은 통계적 연구대상이 되는 전체집합이다.
표본은 연구를 위하여 선택된 모집단의 일부이다.
모수는 모집단을 분석하여 얻어지는 결과수치로 모집단의 특성값이다.( 모평균(𝜇), 모분산(𝜎^2), 모표준편차(𝜎) 등 )
통계량은 표본을 분석하여 얻는 결과수치이다.
확률적 표본추출방법에는 단순무작위표본추출, 체계적표본추출, 비례층화표본추출, 다단계층화표본추출, 군집표본추출이 있다.
비확률적 표본추출방법에는 편의표본추출, 판단표본추출, 할당표본추출, 자발적표본추출이 있다
▣ Descriptive Statistics 기술통계
갭마인더 데이터셋은 국가별, 연도별, 기대수명, 인구수 1인당 GDP 등의 동향을 정리한 데이터셋
중심경향도 : 평균, 중앙값, 최빈값 등
산포도 : 분산, 표준편차, 범위 등
비대칭도 : 왜도, 첨도
중앙값은 관측된 자료의 편중과는 상관없이 최소값부터 최대값까지 나열했을 때 가운데 위치한 값
자료가 2, 4, 7, 8, 10으로 주어졌을 때, 중앙값은 7 (홀수개)
자료가 2, 4, 7, 8, 9,10으로 주어졌을 때, 중앙값은 7.5 (짝수개)
*** 표본분산
모집단을 기준으로 하지 않고, 표본을 선정하여
표본의 개수를 (n-1)로 계산한 분산을 표본분산이라 함
표본의 평균을 알 수 있을 때, 분산을 구하는 경우 전체 표본의 개수에서 1을 뺄 때 더 정확한 분산을 구할 수 있음
표본의 개수에서 1을 뺀 (n-1)을 자유도라고 부름
* 사분위수 구하기
제1사분위수는 누적백분율 25%
제2사분위수는 누적백분율 50%
제3사분위수는 누적백분율 75%
제4사분위수는 누적백분율 100%에 해당하는 값

도수분포표는 빈도를 나타내는 빈도표이다.
▣ Random Variable
사건, 확률변수, 확률, 확률함수의 관계
동전을 두 번 던질때 앞면이 나오는 경우를 기준으로 사건, 확률변수, 확률, 확률함수의 관계를 살펴보자.
동전을 두 번 던졌을 때 발생되는 사건은 HH, HT, TH, TT로 총4가지이다.
앞면이 몇 번 나올 것인가를 기준으로 사건을 분류하면, 확률변수는 HH는 앞면이 2번이므로 2,
HT와TH는앞면이1번이므로1, TT는앞면이나오지않으므로0이된다.
확률변수의 평균 = 기대값
확률함수 : 확률 𝑃를 가진 어떤 사건에 대하여 𝑛번 시행하여 𝑥 번이 나타날 때, 확률변수 𝑥와 이에 대응하는 𝑃 (𝑥)의 관계를 나타내는 함수
▣ Probability Distribution 확률분포
균등분포
이산균등분포
연속균등분포
스톱워치를 작동시킨 후 편안히 잠을 자고 일어나서
시계를 확인했을 때, 분침과 상관없이 초침이 45~55 사이에있을확률을구하시오.
∴ 𝑃 45 ≤ 𝑋 ≤ 55 = 55 − 45 × 1/60 = 1/6
정규분포
- 넓이가 확률값
표준정규분포
***** 시각화 retool
베르누이 분포
= 성공확률 * 실패확률
이항분포
연속적인 베르누이 시행을 통해 표현된 확률분포
성공확률 𝑝 에 대하여 베르누이 시행을 𝑛회 반복한 이항분포를 𝑋~𝐵(𝑛,𝑝)와같이표현함
확률분포란 미래에 일어날 사건에 대하여 확률을 나열한 것을 의미한다.
균등분포란 과거의 경험이 미래를 예측함에 있어 어떠한 영향도 미치지 않고 발생할 가능성이 동일한 분포를 의미한다.
정규분포란 데이터들을 토대로 미래를 예측할 수 있는 분포이다.
베르누이시행이란 서로 반대되는 사건이 일어나는 시행을 반복적으로 실험하는 것을 의미한다.
이항분포란 연속적인 베르누이 시행을 통해 표현된 확률분포를 말한다.
▣ Estimation & Test 추정과 검정
점추정 : 하나의 값으로
구간추정: 최소값과 최대값의 범위로
기술통계: 수집된자료의특성을요약정리하는것이목적
추리통계: 분석된자료를근거로모집단의특성을추론하는것이목적
Estimation(추정치): 모수를 추정하기 위하여 선택된 표본으로부터 구체적으로 도출된 통계량
Estimator(추정량): 표본으로부터 관찰된 값을 토대로 추정치를 계산할 수 있는 함수
표준오차란 ‘표본평균의 표준편차’로서, ‘표본이 참 값인 모평균으로 부터 얼마나 떨어져 있는지를 나타내는 값’
신뢰구간 95, 99% 를 주로 사용
확률과 통계점수의 평균은 50이고 표준오차는 10일 때, 신뢰도 95%, 99%에서 구간추정으로 평균에 대한 모수를 추정하시오.
풀이
신뢰도95%에서구간추정
50 − 1.96 10 ≤𝜇 ≤50 + 1.96 10
∴ 30.4 ≤𝜇 ≤69.6
신뢰도99%에서구간추정
50 − 2.58 10 ≤𝜇 ≤50 + 2.58 10
∴ 24.2 ≤𝜇 ≤75.8
모분산이 없을 때 표본분산을 이용해서 해결
▣ TEST
모수 == 모평균, 모분산 등
귀무가설 : 없다 가설
대립가설 : 있다 가설
Type I, II Error
1종오류: 귀무가설이 참임에도 불구하고, 귀무가설을 기각하는 오류
즉, 실제로 효과가 없는데도 효과가 있다고 하는것
2종오류: 대립가설이 참임에도 불구하고, 대립가설을 기각하는 오류
즉, 실제로 효과가 있는데 효과가 없다고 하는것 ( 덜 위험한 오류 )
*** 유의수준 Significance Level
: 가설검정에서 귀무가설을 기각시키고 대립가설을 채택할 확률을 유의수준이라고 함
유의수준이란 표본으로부터 구한 통계량값을 귀무가설이 참이라는 전제하에서 어느정도로 얻기 힘든 값인지를 나타내는 확률수준을 의미함
*** 유의확률
유의확률을 p-Value 라고 하며, 귀무가설을 기각할 수 있는 최소한의 확률을 의미함
유의수준을 기준으로 유의확률이 유의수준보다 높으면 귀무가설을 채택하고, 낮으면 대립가설을 채택함
유의확률이 클수록 신뢰구간에 포함되고 가설이 채택됨
유의수준을 .05로 두는 이유가 무엇인가요? 처음부터 유의수준 상수치를 바꾸면 안되나요?
=> 연구자가 정하는 것으로 연구자가 정함. 일반적으로 99.5%
=> 의약 쪽은 99.9%로 하는 경우도 있음.
가설검정의 절차
가설 수립 -> 유의수준 결정(알파값 결정) -> 기각역 설정 -> 통계량의 계산 -> 의사결정
가설 검정의 유효기간 - 6개월이 될 수도 있다. 연구자에 따라 다름. 계속해서 차이를 만들어 내므로...
▣ t-test
유의 수준 : 인간환경일 경우 0.05, 생명과 직결되는 경우 0.001과 같이 작아짐.
Two dependent samples t-test 두 종속표본 t검정
Two independent samples t-test 두독립표본t검정
단일표본 t검정이란 모집단의 분산을 알지 못할 때 모집단에서 추출된 표본의 평균과 연구자나 조사자가 이론적 배경이나 경험적 배경에 의해서 설정한 특정한 수를 비교하는 방법이다.
두 종속표본 t검정이란 알지 못하는 각기 다른 두 모집단의 속성인 평균을 비교하기 위하여
두 모집단으로부터 표본들을 추출하여 표본의 평균들을 비교함으로써 모집단의 평균을 비교하는 통계적 방법이다.
독립표본 t검정이란 각기 다른 두모집단의 속성인 평균을 비교하기 위하여, 두 모집단을 대표하는
표본들을 독립적으로 추출하여 표본의 평균들을 비교함으로써 모집단의 유사성을 검정하는 방법이다.
▣ ANOVA 분산 분석
3개 이상의 집단에 대한 평균의 차이를 검정하는 분석 방법임
평균의 차이를 분석하는 방법임에도 불구하고 분산분석이라고 부르게 된 이유는 분산을 비교하여 평균의 차이를 검정하기 때문임
F분포는 두개의 분산에 관한 추론
일원분산분석(one-way ANOVA)은
한 가지 기준이 되는 요인으로 비교하고자 하는 변수의 평균차이가 집단간에 존재하는지를 조사하는 것
이원분산분석(two-way ANOVA)은
두 가지 기준이 되는 요인으로 비교하고자 하는 변수의 평균차이가 집단간에 존재하는지를 조사하는 것
다원분산분석(multi-way ANOVA)은
세 가지 이상의 기준이 되는 요인으로 비교하고자 하는 변수의 평균차이가 집단간에 존재하는지를 조사하는 것
다변량분산분석(multi-variate ANOVA)는
1개 이상이 되는 요인에 대해 비교하고자하는 2개 이상의 변수를 기준으로 집단간에 차이가 있는지를 조사하는 것
One-Way ANOVA
실습
Two-way ANOVA
실습
분산분석이란 분산의 원인이 어디에 있는가를 알아보는 통계적 방법이다.
일원분산분석이란 독립변수가 하나일 때 분산의 원인이 집단간 차이에 기인한 것인지를 분석하는 통계적 방법이다.
이원분산분석이란 두가지 기준이 되는 요인으로 비교하고자하는 변수의 평균차이가 집단간에 존재하는지를 조사하는 것이다.
▣ Correlation Analysis 상관 분석
Pearson’s Correlation Coefficient
Machine Learning Review
요슈아 벤지오
https://www.youtube.com/watch?v=sIFbOP8De0Q
▣ Linear Regression
손실함수에서 오차를 계산할 때는 (𝒕 − 𝒚)𝟐 을 사용함
=> 제곱을 했기 때문에 오차는 언제나 양수이며
정답 𝑡와 계산 값 𝑦의 차가 크다면 제곱에 의한 오차는 더 큰 값을 가지게 되고, 이로써 머신러닝을 학습하기 훨씬 수월해 짐
▣ Gradient Descent 경사하강법
선형회귀란 트레이닝 데이터를 이용하여 데이터의 특성과 상관관계등을 학습하고,
학습결과를 바탕으로 트레이닝 데이터에 없는 미지의 데이터에 대한 결과를 연속적인값(숫자)으로 예측하는 것이다.
머신러닝에서 학습이라는 것은 트레이닝 데이터를 먼저 분석하고 그 데이터의 분포를 가장 잘 나타내는 일차함수의 가중치𝑾, 바이어스𝒃를 찾는과정이라고 할 수 있다.
손실함수에서 오차를 계산할 때는 다음과 같이(𝒕 − 𝒚)𝟐 을사용한다.
▣ Binary Classification
Sigmoid function
Binary Cross Entropy
Maximum Likelihood Estimation
𝐿 𝑇 = 𝑡; 𝑥 = 𝑦^t (1 − 𝑦)^(1-t)
product 기호( ∏ ) : 곱하기
시그마 기호( ∑ ) : 더하기
E(W, b) : 에러
L(T = t;x) 정답에 대한 가능도
이진분류는 트레이닝 데이터의 특성과 그 들 간의 상관관계를 분석하여, 임의의 입력데이터를 사전에 정의된 두 가지 범주 중 하나로 분류할 수 있는 예측 모델을 만드는 과정이다.
로지스틱회귀알고리즘은 ①트레이닝 데이터의 특성과 분포를 나타내는 최적의 직선을 찾고, ②해당 직선을 기준으로 데이터를 위(1)나 아래(0) 또는 왼쪽(1)이나 오른쪽(0) 등으로 분류하는 방법이다.
시그모이드함수는 0과 1사이의 값으로 계산되므로 시그모이드 함수의 결과를 확률로 해석할 수도 있다.
Maximum Likelihood Estimation의 기본 아이디어는 우리가 실험한 결과(관찰치)를 가장 잘 설명해줄 수 있는 가능성이 높은 모수의 추정치로 택하는 방법이다.
이진크로스엔트로피를 사용하면, 손실함수𝐸(𝑊, 𝑏)의 최소값을 가지는 가중치와 편향을 구할 수 있다.
